不同螺杆构型的聚合物塑化过程混合特性分析
波波林 Lv3
  2025-01-11 14:32:38 2025-01-11 14:32   2025-01-11 16:44:50    

不同螺杆构型的聚合物塑化过程混合特性分析

鉴冉冉，谢鹏程，丁玉梅，杨卫民

( 北京化工大学，机电工程学院，北京 100029)

摘要: 螺杆混合性能是影响聚合物塑化质量和均匀性的重要因素之一。采用扭转元件、销钉元件、Maddock 元件及常规螺纹元件，应用计算流体力学软件 Polyflow 对5 种螺杆构型的混合特性进行了数值仿真分析，结合停留时间分布、剪切速率分布、拉伸速率分布、混合指数和非弹性应力张量的第一特征值等参数比较全面地对其混合能力进行了比较。结果表明，5 种螺杆构型流道内物料均以剪切流动为主，Maddock 元件的剪切作用最明显，具有分流功能的结构可以在一定程度上强化对物料的拉伸作用; 2 种扭转元件对于物料的混合效果相对较好，其次是销钉元件和 Maddock元件，最差的是常规螺纹元件。

关键词: 混合性能; 停留时间; 剪切速率; 拉伸速率; 混合效率; 混合指数中图分类号: TP391. 9 文献标识码: A 文章编号: 1001 － 9456( 2018) 06 － 0001 － 04

Comparison of Polymer Mixing Properties Processed by Different Kinds of Screw Configurations

JIAN Ｒanran，XIE Pengcheng，DING Yumei，YANG Weimin

Abstract: The mixing performance of screw was one of the important factors that affected the quality and uniformity of polymer plasticizing． Polymer mixing properties processed by five kinds of screw configurations，namely torsion element，pin element，maddock element and screw element，were simulated and compared through using Polyflow as polymer fluid dynamic software． The mixing ability was compared comprehensively based on residence time distribution，shear rate distribution， stretching rate distribution，mixing index and the first eigenvalue of the extra-stress tensor $T$ ． The results showed that material in the runner of five kinds of screw configurations suffered shear action mainly，and maddock element was of the largest shear action in the runner． The structure with distributary function could strengthen the tensile effect on the material to a certain extent． The mixing effect of two kinds of torsion elements was relatively good，the next was pin element and maddock element， the worst was the conventional screw element．

Keywords: mixing properties; resident time; shear rate; stretching rate; mixing efficiency; mixing index

0 引言

塑料制品越来越多地被用于精密光学器件、生物医学器件等领域，对挤出和注射成型加工中的聚合物塑化混合效果要求也越来越高［1］。由于常规螺杆塑化不均，精密制品容易出现各种质量缺陷，很难达到器件的使用要求［2］。

作为决定制品质量的关键因素之一，聚合物熔体的均匀性很大程度上取决于塑化过程中螺杆混合性能的优劣［3 －4］。目前，设计完成的混炼元件主要分为4 种形式: 分离型、屏障型、分流型以及变流道型［5 －8］。良好的混合性能可以强化传质，使物料的物理性能更加均匀，例如温度、黏度等。强化混合性能的流体流动形式主要有 3 种: 剪切流、拉伸流、扰流或螺旋流，例如，

Maddock 元件的设计原理为剪切流变理论，叶片挤出机［9］的设计原理是拉伸流变理论，销钉元件的设计原理是扰流分流理论，但3 种元件都能达到良好的混合效果。文章将场协同理论引入到聚合物塑化混合过程中，发明了强化径向传质的新型扭转元件［10 －11］，通过扭转曲面和机筒内壁的双重作用实现了物料在流道内的径向翻滚，加速了聚合物的塑化，改善了混合均匀性。

在研究中，文章试图采用计算流体力学软件 Polyflow 对常规螺纹元件、销钉元件、Maddock 元件及扭转元件等 5 种不同构型的塑化混炼结构的混合性能进行模拟和对比分析，从而验证了扭转元件对混合性能的改善程度，为其在挤出和注射成型加工设备中的应用提供了理论参考。

1 理论模型

1. 1 物理模型

扭转元件三维实体模型如图1 所示，将一定长度的某段螺杆沿圆周方向 $n$ 等分设置分割槽，入口处将单股料流分流成多股，出口处将多股料流汇流成单股; 在分割槽内设计2 个相互垂直的 $90^{\circ}$ 扭转曲面，使聚合物在分割棱和机筒的引导下实现扭转，把原先位于分割槽底部的物料移动到分割槽顶部，使聚合物熔体在沿斜面轴向流动的同时发生径向翻滚。

5 种螺杆构型的三维实体模型如图 2 所示，长度和外径均为 $30\mathrm{mm}$ 。螺纹元件螺距为 $30\mathrm{mm}$ ，单个扭转元件长度为 $10\ \mathrm{mm}$ 。


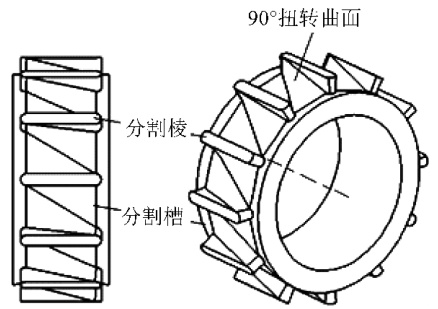
图1 扭转元件物理模型

图2d 是3 个扭转元件的分割棱对齐排列，图 2e 是 3 个扭转元


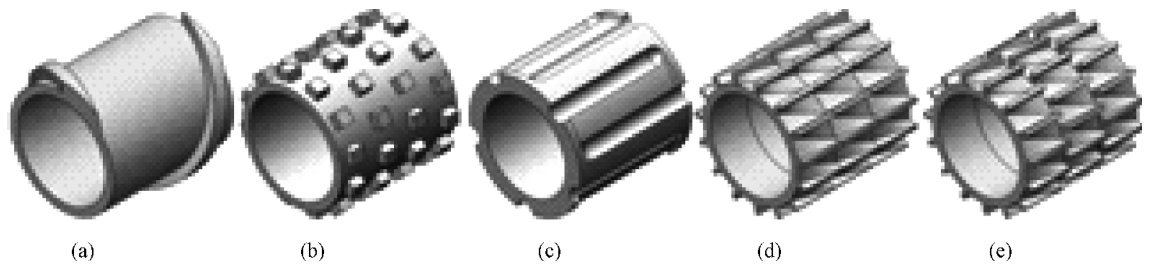
( a) 螺纹元件 ( b) 销钉元件 ( c) Maddock 元件 ( d) 扭转元件 A ( e) 扭转元件 B
图2 5 种螺杆构型的物理模型

件的分割棱交错排列。

1. 2 数学模型和边界条件

结合聚合物的成型理论，做出如下假设: 熔体为不可压缩流体，流动为非等温非稳定流动，熔体在流道中全充满，壁面无滑移且不计惯性力、重力的影响。流体物性参数如表1 所示。

表1 流体物性参数

项目数值
密度p/(kg/m3)900
热导率k/（W/（m·K)）2
定容比热容C,/（J/（kg·K)）20
no /( Pa · s)10 000
n∞ /( Pa · s)100
非牛顿指数n0.75
自然时间入/s0.5
温度系数α/（K-1)2000
绝对零度To/K0
基准温度T。/K473

在以上多种假设的情况下，描述该流场的控制方程如公式( 1) ～ ( 3) 所示。

连续性方程

∂ui∂xi=0 {\frac{\partial u_{i}}{\partial x_{i}}}\,=\,0

动量方程

ρ∂ui∂t+∂p∂xi=∂∂xj(η∂ui∂xj) \rho\,\frac{\partial u_{i}}{\partial t}\,+\,\frac{\partial p}{\partial x_{i}}\,=\,\frac{\partial}{\partial x_{j}}\bigg(\,\eta\,\frac{\partial u_{i}}{\partial x_{j}}\bigg)

能量方程

ρcp(∂T∂t+ui∂T∂xi)=λ∂2T∂xi2+φ \rho\;c_{p}\left(\;\frac{\partial T}{\partial t}\,+\,u_{i}\;\frac{\partial T}{\partial x_{i}}\right)=\,\lambda\;\frac{\partial^{2}\,T}{\partial\;x_{i}^{2}}\,+\,\varphi

本构方程采用 Bird-Carreau 模型和 Arrhenius 模型进行描述，如式( 4) 所示。

η = [ η∞ + ( η0 −η∞)( 1 +λ2 γ˙2)n−12]⋅ \eta~=~[~\eta_{\infty}~+~(~\eta_{0}~-\eta_{\infty})(~1~+\lambda^{2}~\dot{\gamma}^{2})^{\frac{n-1}{2}}]\,\cdot exp[α(1T−T0−1Tα−T0)] \exp\Bigl[\,\alpha\Bigl(\,\frac{1}{T\,-\,T_{\scriptscriptstyle0}}\,-\frac{1}{T_{\scriptscriptstyle\alpha}\,-\,T_{\scriptscriptstyle0}}\Bigr)\Bigr]

式中: η\eta 为表观黏度，Pa⋅s;η0\mathrm{Pa}\cdot\mathrm{s};\eta_{0} 为零剪切黏度，Pa⋅s;η∞\mathrm{Pa}\cdot\mathrm{s};\eta_{\infty} 为无穷大剪切黏度， Pa⋅s;λ\mathrm{Pa}\cdot\mathrm{s} ; \lambda 为自然时间， s;α\mathbf{s};\alpha 为温度系数， K−1{\mathrm{K}}^{-1} ; T0T_{0} 为绝对零度，K; TαT_{\alpha} 为基准温度， K;,n\mathrm{K};,n 为非牛顿指数; γ˙\dot{\gamma} 为剪切速率， s−1\mathrm{s}^{-1} 。

计算中所用到的流动边界条件和热边界条件如表 2 所示，流体与机筒进行恒壁温对流换热。

表2 边界条件

位置流动边界条件热边界条件
流动人口质量流率5kg/h453 K
流动出口自由出口热出口
机筒内表面转速60r/min513 K
螺杆外表面壁面无滑移绝热

2 结果与讨论

2. 1 停留时间分布

停留时间分布是表征混合效果的重要参数，停留时间分布曲线相对靠右，则混合效果越好［12］。在流道入口处随机释放3 000个粒子，通过 Polyflow 软件的 Polystat 统计功能模块，统计这些粒子在流场中的运动情况并进行相应的分析。图3 为 5 种螺杆构型对应流道内粒子的累积停留时间分布及流线轨迹。可以看出，累积停留时间分布曲线从左到右依次是螺纹元件、Maddock 元件、销钉元件/扭转元件 A/扭转元件 B。一般而言，Maddock 元件、销钉元件、2 种扭转元件的累积停留时间分布曲线相差较小。结合 5 种螺杆构型的流线轨迹发现，Maddock 结构、销钉和扭转结构的存在引起了扰流或螺旋流，使粒子的运动历程延长，停留时间增大。


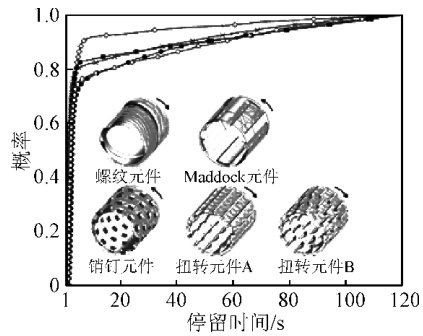
图3 5 种螺杆构型的停留时间分布及流线

2. 2 剪切速率和拉伸速率分布

剪切速率和拉伸速率分别是评价混合元件对物料剪切和拉伸作用的重要参数，剪切作用和拉伸作用均有助于混合。图 4为5 种螺杆构型沿螺杆轴向的平均剪切速率分布。可以看出，Maddock 元件的剪切速率最大，螺纹元件的剪切速率最小; 销钉元件、扭转元件 A 和扭转元件 B 的沿程剪切速率相差较小; 在没有销钉的轴向位置处，剪切速率有所下降。结果与各螺杆构型是相吻合的，螺杆与机筒间隙越小，剪切作用越明显。


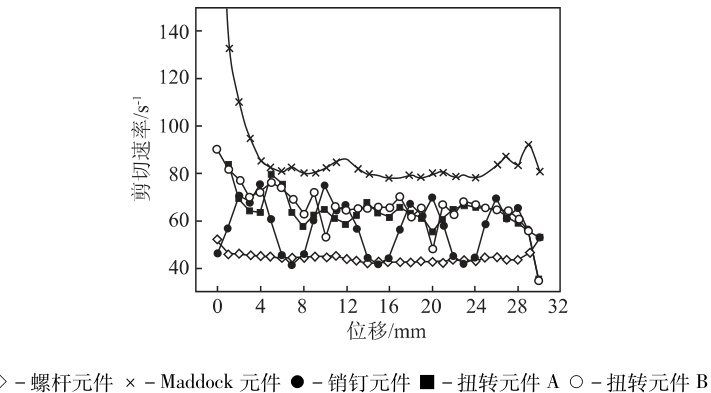
图4 5 种螺杆构型的剪切速率分布

图5 为5 种螺杆构型沿螺杆轴向的平均拉伸速率分布。从拉伸速率的数值上可以看出，5 种螺杆构型对物料均没有明显的拉伸作用。然而，对于扭转元件 B 在单个扭转元件交错连接处和销钉元件在销钉位置处，拉伸速率均有所上升，说明结构对物料的分流作用会产生拉伸效果。


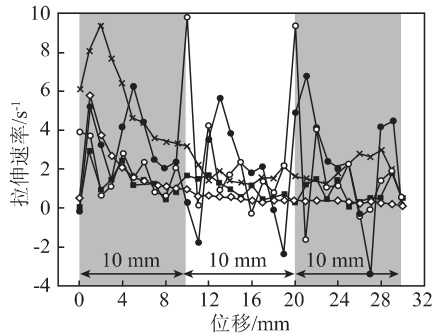
$\diamondsuit$ －螺杆元件 $\times$ － Maddock 元件 ● － 销钉元件 ■ － 扭转元件 A ○ － 扭转元件 B图5 5 种螺杆构型的拉伸速率分布

2. 3 混合效率

瞬时混合效率和时均混合效率是表征分布混合性能的重要参数，表示物料在拉伸作用下面积伸展的程度［13］。图 6 为 5 种螺杆构型瞬时混合效率随着时间的变化曲线。可以看出，5 种螺杆构型的瞬时混合效率从高到低依次是扭转元件 B、扭转元件 A、销钉元件、Maddock 元件、螺纹元件。这说明随着时间的增加，扭转元件对应的瞬态混合效率高于其他元件，使流道内物料受到拉伸作用而混合效果更好。与图 5 所得结果相比较说明，实验中，在拉伸作用没有明显差异的情况下，瞬时混合效率对拉伸作用的效应比截面平均拉伸速率更明显。


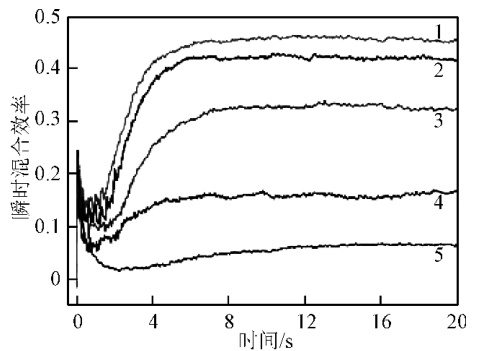
1 － 扭转元件 B 2 － 扭转元件 A 3 － 销钉元件 4 － Maddock 元件 5 － 螺纹元件图6 5 种螺杆构型的瞬时混合效率

图7 为5 种螺杆构型沿螺杆轴向的时均混合效率分布。可以看出，随着轴向位置的增加，5 种螺杆构型的时均混合效率从高到低依次为销钉元件、扭转元件 B、扭转元件 A/Maddock 元件、螺纹元件。对于扭转元件 B，在单个扭转元件连接处，时均混合效率迅速增加，这与图5 所示的结果是一致的，单个扭转元件交错连接处分割棱的分流作用打断了流体微团，产生了拉伸作用，提高了混合效果。


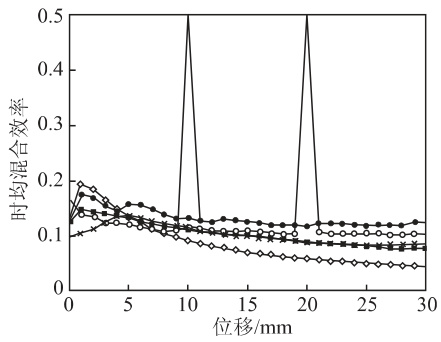
$\diamondsuit$ －螺杆元件 $\times$ － Maddock 元件 ● － 销钉元件 ■ － 扭转元件 $\textrm{A O}-$ 扭转元件 B图7 5 种螺杆构型的时均混合效率

2.4 混合指数和非弹性应力张量的第一特征值

混合指数和非弹性应力张量的第一特征值是表征分散混合性能的重要参数。混合指数的值可以反映流体的流动形式，在0 ～1 的范围内变化，1 代表纯拉伸流动，0. 5 代表简单剪切流动，0 代表简单有旋流动或平移( 刚体运动) ［14 －15］。而非弹性应力张量的第一特征值是使粒子发生破碎的主要应力。图 8 为 5种螺杆构型沿螺杆轴向的混合指数分布情况。可以看出，5 种螺杆构型的混合指数主要集中在 0. 5 左右，说明物料主要以剪切流动为主。对于扭转元件 B，混合指数在单个扭转元件交错连接处出现波峰，与上述图5 和图7 的结果较为一致。

图9 为5 种螺杆构型的非弹性应力张量第一特征值。从图中可以得到，该应力第一特征值从高到低依次是 Maddock 元件、扭转元件 A/扭转元件 B/销钉元件、螺纹元件。其中，2 种扭转元件和销钉元件的变化趋势相差较小。因为扭转元件与销钉元件均是基于扰流或螺旋流的作用机制对混合产生影响的，对粒子的破碎作用相对于强剪切结构 Maddock 元件要弱，但是高于常规螺纹元件。


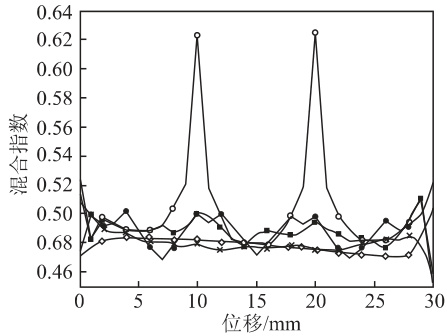
$\diamondsuit$ －螺杆元件 $\times$ － Maddock 元件 $\bullet$ －销钉元件 $\mid-$ 扭转元件 A ○ －扭转元件 B
图8 5 种螺杆构型的混合指数


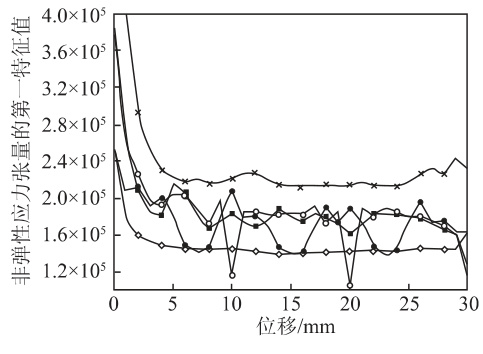
图9 5 种螺杆构型的非弹性应力张量第一特征值

3 结论

文章通过停留时间分布、剪切速率、拉伸速率、混合效率、混合指数、非弹性应力张量的第一特征值等参数对 5 种螺杆构型的混合性能进行了分析和探讨，获得了如下结论:

  1. 5 种螺杆构型对物料的混合效果相对较好的是扭转元件和销钉元件，其次是 Maddock 元件，最后是螺纹元件。新型螺杆结构通过在流道中引入螺旋流，可以增加粒子的运动历程和停留时间，使混合效果更加充分。

  2. Maddock 元件的剪切速率最大，其次是扭转元件和销钉元件，最后是螺纹元件。螺杆与机筒的间隙越小，剪切作用越大，通过增加微小间隙的面积，可以强化其对物料的剪切作用。此外，具有分流功能的结构也可以强化其对物料的拉伸作用。

  3. 5 种螺杆构型的瞬时混合效率从高到低依次是扭转元件B、扭转元件 A、销钉元件、Maddock 元件、螺纹元件。综合比较，扭转元件对物料的混合效果要优于销钉元件、Maddock 元件和螺纹元件。扭转元件分割棱的交错排列优于分割棱对齐排列。

  4. 5 种螺杆构型的的混合指数主要集中在 0. 5 左右，流动形式主要以剪切流为主。其中，Maddock 元件对物料的破碎作用相对较好，扭转元件和销钉元件次之，螺纹元件最差。

参考文献:

［1］ 余东泉，何亚东，杨昆晓，等． 三螺杆挤出机剪切 － 拉伸作用的理论分析［J］． 塑料，2018，47( 2) : 119 － 121．
［2］ HOPMANN C，FISCHEＲT． New plasticising process for increasedprecision and reduced residence times in injection moulding of microparts［J］． CIＲP Journal of Manufacturing Science and Technology，2015，9: 51 － 56．
［3］ POTENTE H，TOBBEN W H． Improved design of shearing sectionswith new calculation models based on 3D finite-element simulations［J］． Macromolecular Materials and Engineering，2002，287 ( 11 ) :808 － 814．
［4］ SIKOＲA J W，SAMUJLO B． Investigation of the poly( vinyl chloride)extrusion process using a feed throat with a feed pocket［J］． PolymerEngineering and Science， $2014,54({:9}):2037:-2045.$
［5］ CHEN J，DAI P，YAO H，et al． Numerical analysis of mixing performanceof mixing section in pin-barrel single-screw extruder［J］． Journal ofPolymer Engineering， $2011,,31(,1):53,-62$ ．
［6］ ＲAUWENDAAL C． New developments in mixing and screw design［J］． Plastics，Additives and Compounding， $2008,,10(,6):32,-36$ ．
［7］ JIAN Ｒ，YANG W，CHENG L，et al． Numerical analysis of enhancedheat transfer by incorporating torsion elements in the homogenizingsection of polymer plasticization with the field synergy principle［J］．International Journal of Heat and Mass Transfer，2017，115，Part A:946 － 953．
［8］ TAGUCHI T，SAITO H． Effects of plasticization and hydrostatic pressureon tensile properties of PMMA under compressed carbon dioxide andnitrogen ［J ］． Journal of Applied Polymer Science，2016，133( 20) : 43431．
［9］ 华南理工大学． 基于拉伸流变的高分子材料塑化输运方法及设备: 中国，CN100496927C［P］． 2009 － 06 － 10．
［10］ 北京化工大学． 聚合物熔体微积分强化传热与混炼塑化挤出机:中国，CN103753793A［P］． 2014 － 04 － 30．
［11］ 鉴冉冉，谢鹏程，杨卫民． 基于场协同原理的聚合物塑化过程数值分析［J］． 工程热物理学报，2017，38( 2) : 281 － 288．
［12］ KIM S J，KWON T H． Enhancement of mixing performance of single-screw extrusion processes via chaotic flows: Part I． Basic concepts andexperimental study［J］． Advances in Polymer Technology，1996，$15(\mathrm{1}):41-54$ ．
［13］ 李彬． 单螺杆混沌挤出过程混合机理与实验研究［D］． 江门: 五邑大学，2014．
［14］ 胡建鹏，杜瑶雪，吴希智． 聚合物新型混合分散装置塑化过程模拟分析［J］． 五邑大学学报: 自然科学版，2012，26( 4) : 37 － 41．
［15］ 王天书，郝永辉，朱向哲． 螺棱数对三螺杆挤出机混合段流动和混合特性的影响［J］． 塑料工业，2015，43( 12) : 69 － 73．

( 本文编辑 GYJ)

 评论
  1. 1. 不同螺杆构型的聚合物塑化过程混合特性分析
    1. 1.1. Comparison of Polymer Mixing Properties Processed by Different Kinds of Screw Configurations
    2. 1.2. 0 引言
    3. 1.3. 1 理论模型
      1. 1.3.1. 1. 1 物理模型
      2. 1.3.2. 1. 2 数学模型和边界条件
    4. 1.4. 2 结果与讨论
      1. 1.4.1. 2. 1 停留时间分布
      2. 1.4.2. 2. 2 剪切速率和拉伸速率分布
      3. 1.4.3. 2. 3 混合效率
      4. 1.4.4. 2.4 混合指数和非弹性应力张量的第一特征值
    5. 1.5. 3 结论
  2. 2. 参考文献: